En el campo de la probabilidad y la estadística, el Teorema de Bayes es una herramienta fundamental para calcular la probabilidad de un evento dado cierta evidencia. Este teorema, desarrollado por el matemático inglés Thomas Bayes, permite actualizar nuestras creencias iniciales sobre un evento a medida que obtenemos nueva información.

El Teorema de Bayes es especialmente útil cuando nos enfrentamos a situaciones de incertidumbre, donde no conocemos con certeza las probabilidades de los eventos. En estos casos, podemos utilizar el teorema para ajustar nuestras estimaciones y tomar decisiones informadas.

En este artículo, exploraremos en detalle el Teorema de Bayes y su aplicación en diferentes contextos. Veremos cómo se puede utilizar para calcular la probabilidad de un evento condicionado a cierta evidencia, y cómo se relaciona con otros conceptos fundamentales de la probabilidad, como la regla de la multiplicación y la regla de la suma.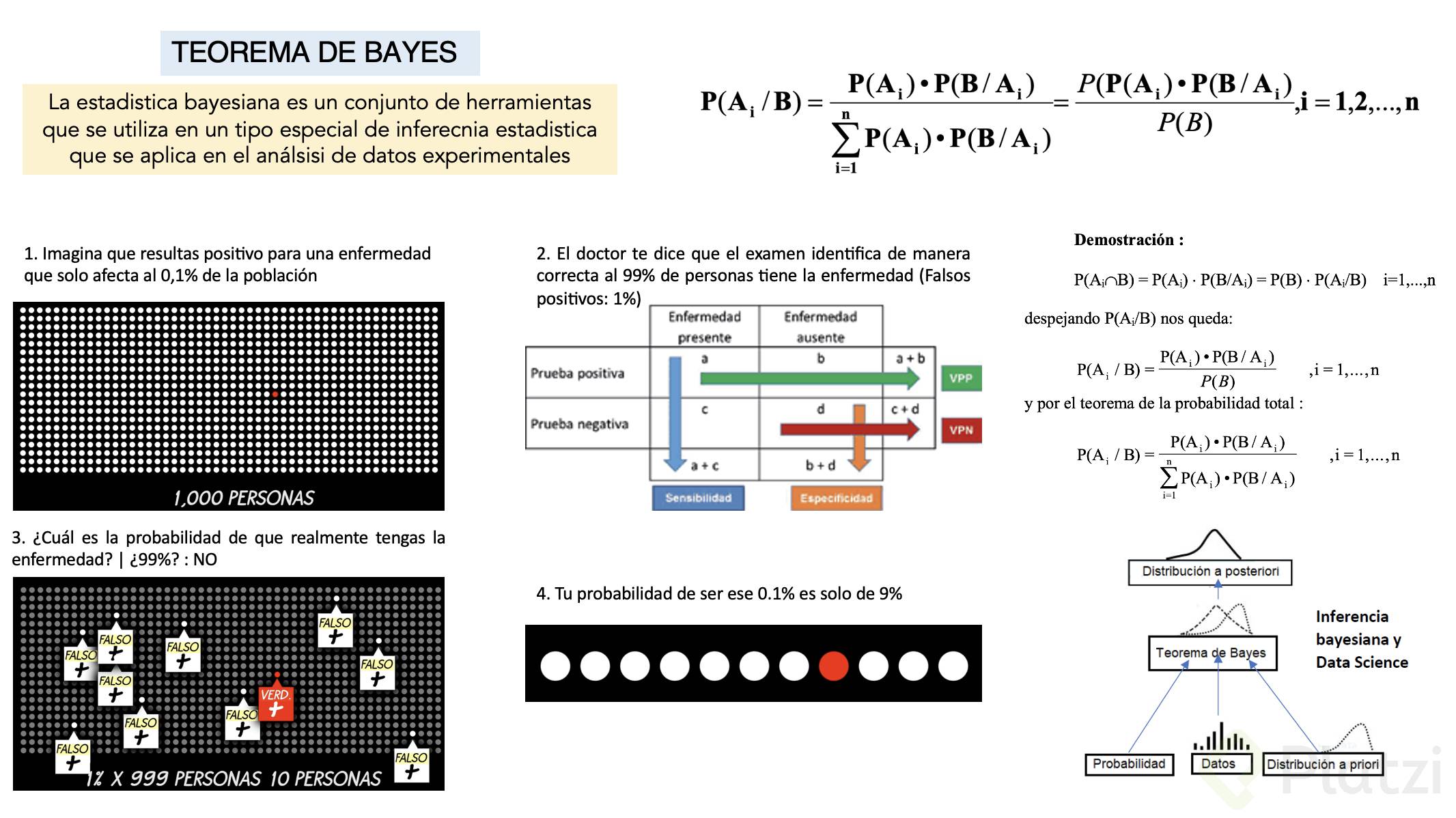

Teorema de Tales

El Teorema de Tales es un concepto fundamental en geometría que establece una relación entre segmentos de rectas paralelas. Este teorema fue descubierto por el matemático griego Tales de Mileto en el siglo VI a.C. y ha sido utilizado desde entonces para resolver problemas geométricos.

Según el Teorema de Tales, si trazamos tres rectas paralelas que intersectan a dos transversales, los segmentos que se forman en una de las transversales son proporcionales a los segmentos correspondientes en la otra transversal. En otras palabras, si tenemos dos segmentos en una transversal y conocemos la proporción entre ellos, podemos utilizar el Teorema de Tales para encontrar la proporción correspondiente en la otra transversal.

Este teorema es especialmente útil en la resolución de problemas de semejanza de triángulos, ya que nos permite encontrar medidas desconocidas utilizando las proporciones entre los segmentos. Además, el Teorema de Tales también se aplica en la resolución de problemas de trigonometría y en la construcción de figuras geométricas.

Introducción al Teorema de Bayes

El Teorema de Bayes es un concepto fundamental en la teoría de la probabilidad y estadística. Fue desarrollado por el matemático inglés Thomas Bayes en el siglo XVIII y ha sido ampliamente utilizado en diversos campos, desde la medicina hasta la inteligencia artificial.

Este teorema permite actualizar la probabilidad de un evento dado, a partir de la información previa y la evidencia nueva que se va obteniendo. Es especialmente útil cuando se trabaja con incertidumbre y se necesitan tomar decisiones basadas en datos limitados.

El Teorema de Bayes se basa en la idea de que la probabilidad de un evento A, dado que ha ocurrido un evento B, se puede calcular a partir de la probabilidad de que ocurra el evento B, dado que ha ocurrido el evento A, multiplicado por la probabilidad de que ocurra el evento A, dividido por la probabilidad de que ocurra el evento B.

Aplicaciones del Teorema de Bayes

El Teorema de Bayes es una herramienta fundamental en el campo de la probabilidad y la estadística, y tiene una amplia gama de aplicaciones en diversos campos. Una de las aplicaciones más comunes del Teorema de Bayes es en el campo de la medicina, donde se utiliza para calcular la probabilidad de que un paciente tenga una enfermedad en función de los síntomas que presenta.

Por ejemplo, supongamos que un paciente presenta síntomas como fiebre, tos y dolor de garganta. Utilizando el Teorema de Bayes, los médicos pueden calcular la probabilidad de que el paciente tenga una enfermedad específica, como la gripe, en función de la prevalencia de la enfermedad en la población y la probabilidad de que una persona con la gripe presente esos síntomas.

Otra aplicación del Teorema de Bayes se encuentra en el campo de la inteligencia artificial y el aprendizaje automático. En este contexto, el Teorema de Bayes se utiliza para actualizar las creencias o probabilidades sobre un evento en función de nueva información o evidencia. Esto es especialmente útil en problemas de clasificación, donde se busca determinar la clase o categoría a la que pertenece un objeto o dato.

Limitaciones del Teorema de Bayes

El Teorema de Bayes es una herramienta poderosa en el campo de la probabilidad y la estadística, pero también tiene sus limitaciones. Una de las principales limitaciones es que se basa en la suposición de que tenemos información completa y precisa sobre los eventos y las probabilidades involucradas. Sin embargo, en la vida real, a menudo nos enfrentamos a situaciones de incertidumbre donde no tenemos toda la información necesaria.

Otra limitación del Teorema de Bayes es que asume que los eventos son independientes entre sí. Esto significa que la ocurrencia de un evento no afecta la probabilidad de que ocurra otro evento. Sin embargo, en muchos casos, los eventos están interrelacionados y la ocurrencia de uno puede influir en la probabilidad de que ocurra otro.

Además, el Teorema de Bayes se basa en la suposición de que las probabilidades son constantes a lo largo del tiempo. Sin embargo, en la realidad, las probabilidades pueden cambiar con el tiempo debido a factores externos o nuevas evidencias. Por lo tanto, es importante tener en cuenta que el Teorema de Bayes puede no ser aplicable en situaciones donde las probabilidades son variables.

El Teorema de Bayes en la vida cotidiana

El Teorema de Bayes es una herramienta matemática que nos permite actualizar nuestras creencias o probabilidades en función de nueva información. Aunque puede sonar complicado, este teorema tiene aplicaciones prácticas en nuestra vida cotidiana.

Por ejemplo, imagina que estás esperando el resultado de un examen médico para determinar si tienes una enfermedad. Antes de recibir los resultados, tienes una cierta probabilidad de tener la enfermedad, basada en factores como tus síntomas y antecedentes familiares. Sin embargo, una vez que obtienes los resultados del examen, puedes utilizar el Teorema de Bayes para actualizar tu probabilidad de tener la enfermedad en función de la precisión del examen y los resultados obtenidos.

El Teorema de Bayes también se utiliza en campos como la inteligencia artificial y el aprendizaje automático. Por ejemplo, en el reconocimiento de voz, se utiliza para calcular la probabilidad de que una determinada secuencia de sonidos corresponda a una palabra específica. Esto permite a los sistemas de reconocimiento de voz mejorar su precisión a medida que reciben más datos y actualizan sus probabilidades.

El Teorema de Bayes en la medicina

El Teorema de Bayes es una herramienta fundamental en el campo de la medicina, ya que permite calcular la probabilidad de que un paciente tenga una enfermedad en base a los síntomas que presenta y la prevalencia de la enfermedad en la población. Este teorema se basa en la idea de que la probabilidad de un evento puede ser actualizada a medida que se obtienen nuevos datos.

Por ejemplo, supongamos que un paciente presenta síntomas como fiebre, tos y dolor de garganta, y queremos determinar la probabilidad de que tenga gripe. Para aplicar el Teorema de Bayes, necesitamos conocer la prevalencia de la gripe en la población, así como la probabilidad de que una persona con gripe presente esos síntomas.

Una vez que tenemos esta información, podemos utilizar el Teorema de Bayes para calcular la probabilidad de que el paciente tenga gripe. Este cálculo se realiza teniendo en cuenta la probabilidad de que una persona tenga gripe (prevalencia), la probabilidad de que una persona sin gripe presente los síntomas (falsos positivos) y la probabilidad de que una persona con gripe presente los síntomas (verdaderos positivos).

El Teorema de Bayes en la inteligencia artificial

El Teorema de Bayes es una herramienta fundamental en la inteligencia artificial que permite calcular la probabilidad de un evento dado ciertos datos o evidencias. Este teorema se basa en la idea de que la probabilidad de un evento puede ser actualizada a medida que se obtienen nuevos datos.

En el campo de la inteligencia artificial, el Teorema de Bayes se utiliza en diversas aplicaciones, como el reconocimiento de voz, la detección de spam en correos electrónicos y la clasificación de imágenes. Por ejemplo, en el reconocimiento de voz, el Teorema de Bayes se utiliza para calcular la probabilidad de que una secuencia de sonidos corresponda a una determinada palabra o frase.

La importancia del Teorema de Bayes en la inteligencia artificial radica en su capacidad para manejar la incertidumbre y actualizar las probabilidades a medida que se obtienen nuevos datos. Esto permite a los sistemas de inteligencia artificial tomar decisiones más informadas y precisas, mejorando su rendimiento y eficiencia.

El Teorema de Bayes en la economía

El Teorema de Bayes es una herramienta fundamental en el campo de la economía, ya que permite analizar y tomar decisiones en situaciones de incertidumbre. Este teorema se basa en la idea de que la probabilidad de un evento depende de la información previa que se tenga sobre el mismo.

En el contexto económico, el Teorema de Bayes se utiliza para calcular la probabilidad de que ocurra un evento dado, teniendo en cuenta la información disponible. Por ejemplo, en el análisis de riesgo financiero, se puede utilizar este teorema para estimar la probabilidad de que una inversión sea rentable, considerando factores como el rendimiento histórico, las condiciones del mercado y las expectativas futuras.

Además, el Teorema de Bayes también es utilizado en la economía para realizar pronósticos y tomar decisiones estratégicas. Por ejemplo, en el análisis de demanda de un producto, se puede utilizar este teorema para estimar la probabilidad de que los consumidores compren dicho producto, considerando variables como el precio, la calidad, la disponibilidad y las preferencias del consumidor.

El Teorema de Bayes en la estadística

El Teorema de Bayes es un concepto fundamental en la estadística que permite calcular la probabilidad de un evento dado cierta evidencia. Fue desarrollado por el matemático y estadístico inglés Thomas Bayes en el siglo XVIII y ha sido ampliamente utilizado en diversos campos, como la medicina, la inteligencia artificial y la economía.

Este teorema establece que la probabilidad de que ocurra un evento A, dado que ha ocurrido un evento B, se puede calcular a partir de la probabilidad de que ocurra el evento B, dado que ha ocurrido el evento A, y la probabilidad de que ocurra el evento A sin tener en cuenta el evento B. En otras palabras, el Teorema de Bayes permite actualizar la probabilidad de un evento a medida que se obtiene nueva información.

La fórmula del Teorema de Bayes es la siguiente:

P(A|B) = (P(B|A) * P(A)) / P(B)

Donde P(A|B) es la probabilidad de que ocurra el evento A dado que ha ocurrido el evento B, P(B|A) es la probabilidad de que ocurra el evento B dado que ha ocurrido el evento A, P(A) es la probabilidad de que ocurra el evento A sin tener en cuenta el evento B, y P(B) es la probabilidad de que ocurra el evento B sin tener en cuenta el evento A.

El Teorema de Bayes en la probabilidad

El Teorema de Bayes es un concepto fundamental en la teoría de la probabilidad y se utiliza para actualizar la probabilidad de un evento dado cierta evidencia. Fue desarrollado por el matemático y estadístico inglés Thomas Bayes en el siglo XVIII y ha sido ampliamente utilizado en diversos campos, como la medicina, la inteligencia artificial y la economía.

El Teorema de Bayes establece que la probabilidad de un evento A dado un evento B se puede calcular utilizando la siguiente fórmula:

P(A|B) = (P(B|A) * P(A)) / P(B)

Donde P(A|B) es la probabilidad de que ocurra el evento A dado que ha ocurrido el evento B, P(B|A) es la probabilidad de que ocurra el evento B dado que ha ocurrido el evento A, P(A) es la probabilidad inicial del evento A y P(B) es la probabilidad inicial del evento B.

El Teorema de Bayes es especialmente útil cuando se trabaja con incertidumbre, ya que permite actualizar las probabilidades a medida que se obtiene nueva información. Esto es especialmente relevante en situaciones en las que la información inicial es limitada o ambigua, y se requiere una toma de decisiones basada en la evidencia disponible.

El Teorema de Bayes en la toma de decisiones

El Teorema de Bayes es una herramienta fundamental en la teoría de la probabilidad y se utiliza ampliamente en la toma de decisiones bajo incertidumbre. Este teorema permite actualizar nuestras creencias o probabilidades iniciales en función de nueva información o evidencia.

En la toma de decisiones, a menudo nos encontramos con situaciones en las que no conocemos con certeza el resultado de un evento. En lugar de tener información completa, solo tenemos probabilidades o creencias iniciales sobre los posibles resultados. El Teorema de Bayes nos permite actualizar estas probabilidades a medida que obtenemos nueva información, lo que nos ayuda a tomar decisiones más informadas y precisas.

El Teorema de Bayes se basa en la idea de que nuestras creencias iniciales, también conocidas como probabilidades a priori, pueden ser modificadas por la evidencia o información adicional que obtenemos. Al combinar nuestras creencias iniciales con la nueva información, podemos obtener probabilidades a posteriori, que representan nuestras creencias actualizadas después de considerar la evidencia.

El Teorema de Bayes en la teoría de juegos

La teoría de juegos es un campo de estudio que analiza las decisiones estratégicas tomadas por diferentes agentes en situaciones de interacción. En este contexto, el Teorema de Bayes juega un papel fundamental al permitir calcular la probabilidad de que un jugador tome una determinada acción, dado el conocimiento que tiene sobre las acciones de los demás jugadores.

El Teorema de Bayes establece una relación entre la probabilidad condicional y la probabilidad inversa. En el contexto de la teoría de juegos, esto significa que podemos calcular la probabilidad de que un jugador tome una acción, dado el conocimiento que tiene sobre las acciones de los demás jugadores, utilizando la información disponible sobre las acciones pasadas y las estrategias utilizadas por los demás jugadores.

Este enfoque probabilístico permite modelar de manera más realista las interacciones entre los jugadores y tomar decisiones estratégicas más informadas. Al utilizar el Teorema de Bayes, los jugadores pueden actualizar sus creencias sobre las acciones de los demás jugadores a medida que se desarrolla el juego, lo que les permite ajustar sus propias estrategias y maximizar sus posibilidades de éxito.

Si deseas seguir leyendo, puedes aprender sobre Fórmula de Torricelli